ZK-SNARK Verifiable Machine Learning
1. What is a ZK-SNARK?
Chances are you've encountered these terms frequently in articles about blockchain, web 3, layer 2, fully-on-chain games, etc. If you search for "ZK-SNARK" on Google, you might come across an explanation like this: The acronym ZK-SNARK stands for Zero-Knowledge Succinct Non-Interactive Argument of Knowledge and refers to a proof construction where one can prove possession of certain information. This can still be very confusing. So, let's break down each word and attempt to provide an informal explanation.
Zero-Knowledge: The prover can convince the verifier that a statement is true without revealing any information beyond the validity of the statement itself.
Succinct: Proofs can be verified within a few milliseconds, with a proof length of only a few hundred bytes, even for statements about programs that are very large. Technically speaking, if the scale of a statement is C, then the verification time is at most O(log C), and the proof size is also at most O(log C).
Non-Interactive: Proofs can be verified offline at any time once they are generated by the prover. There isn't any interactive process between the verifier and the prover.
Argument of Knowledge: There exists at least one solution if the statement is true, and the verifier will accept it; otherwise, the verifier will reject it.
2. How to build ZK-SNARK?
Almost every ZK-SNARK consists of three parts: arithmetization, a proof system, and a commitment scheme.
Arithmetization: What the prover wants to prove in practice is that they have run some kind of program or algorithm with their private input data, and the public data they claimed is exactly the output data of this program or algorithm. However, in a ZK-SNARK system, which builds its security entirely on algebra, all programs or algorithms need to be represented by some polynomial equations. These polynomial equations should be satisfied if the input data and output data are true, as the prover claimed. So, the problem here is how to convert different programs and algorithms into polynomial equations.
Let us take a look at how a program is executed in a computer. Although there are hundreds of different programming languages, they will ultimately be compiled into some kind of assembly language. Then the CPU or GPU would run this assembly language. The CPU or GPU is actually composed of some transistor gates, such as AND, OR, NOT. In the end, your program is actually decomposed into these logic gates.
In ZK-SNARK, we use the same idea. We use "gates" to represent any program or algorithm. But unlike CPU, we use arithmetic gates (e.g., ADD, MULTI) rather than boolean logic gates (e.g., AND, OR, NOT) because arithmetic gates could be more easily converted to polynomials by interpolation. That is why we often call the gates a "circuit".
Proof System: After arithmetization, the prover needs to show the verifier that they do know a set of solutions that satisfy the polynomial equation. They need to generate a ZK-SNARK proof for the verifier. People often use different Interactive Oracle Proofs to do this, and the interactive parts could be transformed into non-interactive by the Fiat-Shamir transformation if they are public-coin.
Commitment Scheme: A commitment scheme works roughly like this: A prover claims that they have a sentence, but they don't want to show it to the verifier right now. So they write it on a note and put this note in a locked box. Then they send this box to the verifier. Because the box is locked, the verifier can't know anything inside it. At some point in the future, the prover sends a key to the verifier so that they can open the box and verify the sentence. There are two properties of a commitment: Binding, once the sentence is committed, the prover can't tamper with it anymore; Hiding, the verifier can't know anything in the box until the prover opens it, in other words, it's zero knowledge. In reality, the commitment is an encryption process, say, representing a polynomial with a group element. When the verifier asks the prover to open it, with some properties of the group (like pairing), they needn't decrypt the commitment. The commitment scheme achieves zero-knowledge, and it's also a computational burden because of the operation of group elements.
3. ZK-SNARK Programmability
After the discussion in Sections 1 and 2, you probably know what a ZK-SNARK is and what the components of an ideal ZK-SNARK are. There are many different ZK-SNARK protocols available if you look through Google. Now, the question is: How could we use a ZK-SNARK protocol to prove our idea or demand? The answer is as the following workflow shows:
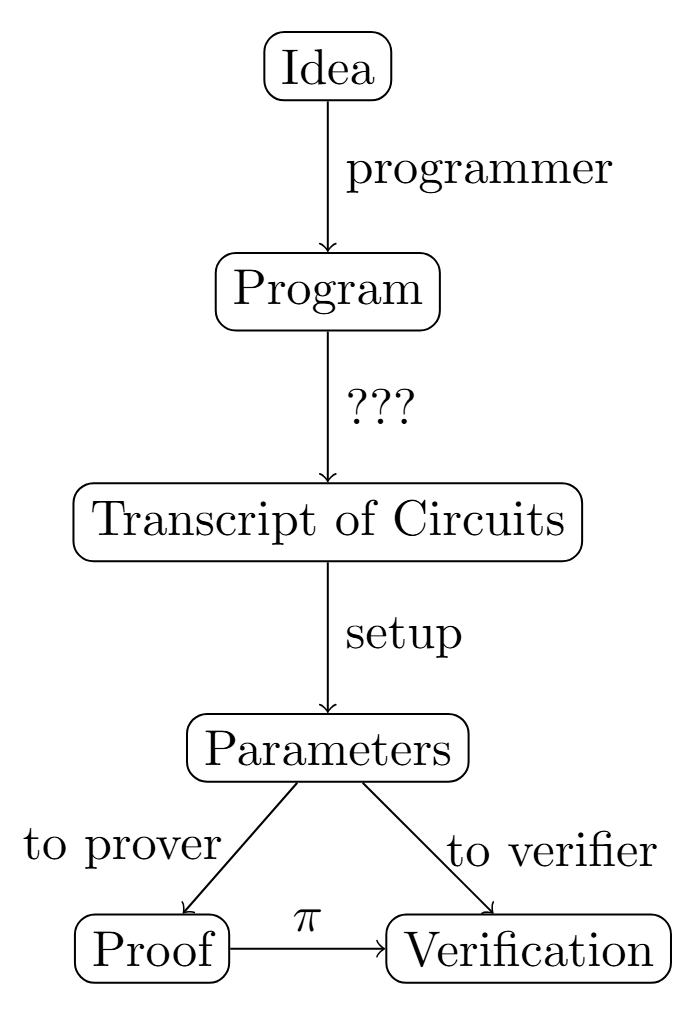
The first step is that we need to convert our idea into some kind of computer program, which is easy to achieve. However, as mentioned in the last section, ZK-SNARKs use arithmetic gates to describe the program. There is a significant gap between a program (e.g., Python, C++) and circuits. So, the second step is to use some kind of a "compiler" to help us translate these programs into circuits or use some "circuit program languages" to depict the idea. Well, there are three different ways to bridge this gap.
We could use some hardware description languages (HDL) that are used to design integrated circuits (like CPU, GPU) to program the idea. Remember that both are constructed with "gates." Circom is one of the most representative HDL languages and is widely used, especially in some scenarios without a frequently trusted setup.
The other way is using libraries built with developers familiar with program languages, such as Bellman (Rust) and Gadgetlib (C++). The pros of libraries are that developers don't need to learn a new HDL language, which is quite distinct from computer programming languages. However, we still have to deal with the gates and constraints in the circuits.
The last method is "program language + compiler." Developers could directly use some new programming languages to code their ideas without dealing with the circuits. But using this high-level programming language always brings some trade-offs and often results in worse performance compared with the two previous methods.
| Language Type | Standalone Language | Not Standalone Language |
|---|---|---|
| Circuit | HDL | Library |
| Program | PL + Compiler |
4. Verifiable Machine Learning
As ML models have increased in capabilities and accuracy, so has the complexity of their deployments. Increasingly, ML model consumers are turning to service providers to serve the ML models in the ML-as-a-service (MLaaS) paradigm. As MLaaS proliferates, a critical requirement emerges: how can model consumers verify that the correct predictions were served, in the face of malicious, lazy, or buggy service providers? To address this challenge, verifiable machine learning (VML) has emerged. From the perspective of AI service providers, the training process of models spends a prohibitive amount of time and money, so the parameters of a trained model should be a valuable asset of the company and ensure that it will not be leaked in the process of usage or verification. While verifying machine learning by ZK-SNARKs could perfectly solve this problem.
How to generate a ZK-SNARK for a machine learning model? The intuitive idea is to use the methods and tools we discussed in the last section. For instance, use Circom to "translate" a machine learning model into circuits and generate corresponding proof. Of course, you can do this, but recall we mentioned the properties in Section 1 that ZK-SNARK only requires the verification time to be short and normally the proof time is super long. For example, directly proving a Twitter recommendation algorithm with ZK-SNARK takes about 6 hours. This way is impractical.
There are two methods we could solve this problem along this line of thought. Either we use a more "powerful" ZK-SNARK protocol, or we make the model more suitable for ZK-SNARKs. Considering users usually don't want to compromise the performance of the model, it seems the only way is developing a more powerful ZK-SNARK protocol aimed at machine learning models.
Halo2 is a ZK-SNARK protocol used in Zcash. The setup process is transparent, and the prover time is linear with the circuit size. Most importantly, because of the lookup-tables and customer-gates in plonkish arithmetization, it's very efficient when dealing with the non-linear parts (e.g., relu, maxpool) in machine learning models. Actually, many tools and frameworks are based on Halo2. One is EZKL, a library and command-line tool for doing inference for deep learning models and other computational graphs in a ZK-SNARK. It focuses on programs that are expressed as PyTorch AI/ML models and other computational graphs, can be used directly from Python. The proofs can be trusted by anyone with a copy of the verifier and verified directly on Ethereum and compatible chains. Another example is ZKML, a framework for constructing proofs of ML model execution in ZK-SNARKs. With ZKML, you could generate proofs of your model and data in TFLite format.
As we mentioned before, Circom is a widely used HDL language in ZK-SNARKs. Although the backend protocols (e.g., Groth16, Plonk) of Circom are not as efficient as Halo2, many developers still choose Circom considering the fast verification speed and shortest proof, especially when trusted setup is not a problem. Circomlib-ml is a library in Circom used for machine learning. Developers can use circuit templates in this library easily when building a circuit for some models. However, the types and numbers of circuits in this library are very limited, which can be hardly used in large models. Keras2circom is another Python tool that transpiles a tf.keras model into a Circom circuit using circomlib-ml.
Last but not least, we want to introduce a method that combines some characteristics of machine learning with a specific ZK-SNARK protocol. ZKCNN is a protocol aimed at CNN models. In this model, convolution, a very common operation in CNN, could be perfectly proved and verified by the sumcheck proof system. We'll discuss this in the next chapter.
Reference
- Zero Knowledge Proofs Mooc: https://zk-learning.org/
- ZKCNN paper: https://eprint.iacr.org/2021/673
- ZKML community: https://github.com/zkml-community/awesome-zkml
- Daniel Kang's Medium: https://medium.com/@danieldkang
- Daniel Kang's Paper: https://arxiv.org/abs/2210.08674