The random number has been used for everything from cryptography to lotteries and games. Blockchains also have a close relationship with randomness because they seek fairness from it. The widely deployed Proof-of-Work consensus protocol is built on a cryptographical quest that searches for specific random values. Many flourishing dapps, such as on-chain lottery or NFT blind boxes, rely on unbiased random inputs to provide a more credible experience. Therefore, ARPA would like to build a secure, robust, and verifiable decentralized random number generator (RNG) to serve essential randomness to the blockchain world.
Trustless Randomness
Either in the physical world or the cyber world, there are many methods to produce randomness. At high-level, these ways can be categorized into two kinds, truly random ones, and pseudo random ones. Truly random number leverages physical noise in the real world, which is not practical to use on chain. In terms of the pseudo random number, there are many alternative algorithms, like public keyed hash message authentication code (HMAC) and threshold signature. To determine the primitive used for yielding random numbers, we will first look at the fundamental properties of an RNG.
Uniqueness & Determinacy
Repeatedly generating and selecting a biased random number is not expected for the security-sensitive applications that rely on randomness. The adversaries would carefully choose the random number to extract profit. An RNG with uniqueness can mitigate this risk, which means that anyone consuming the random number can verify its legitimacy with certainty. As for the decentralized RNG, uniqueness ensures that the random number is only related to the entire set of generation nodes but not the subset.
Uniqueness is a stricter requirement than determinacy. Determinacy only requires that the random generation procedure involves no randomness. In comparison, uniqueness needs to convince the consumers that the random number is not biased. For example, ECDSA can be redefined to satisfy determinacy but not uniqueness.
Non-interactiveness
In the blockchain, it is natural to generate random numbers in a decentralized way. However, the communication overhead will become a limitation or a single point of failure of the whole system. It is expected to involve only one round of one-way communication for each node during the random number generation. It implies that random number shares contributed by parties should be aggregatable in an asynchronous way like multi-signature.
Availability
The availability of base services like RNG really matters. In the meantime, we cannot count on the uptime of the decentralized system nodes. Therefore, the algorithm should provide a perfect availability based on the unstable computation nodes. Threshold signature or multi-sig are ideal methods that tolerate faults and downtime, especially the asynchronous ones. The lower proportion of the required nodes in the group, the higher the availability.
Threshold BLS Signature
Considering the above mentioned factors, we finally choose the threshold BLS signature as the long-term algorithm generating random numbers. First of all, ETH 2.0 will switch to the BLS12–381 standard as the primary signature scheme, which facilitates BLS-based applications running on Ethereum. Any other public blockchain that supports the BLS scheme will also be compatible with our design. Secondly, BLS is an instance of pairing-based cryptography. The bilinearity of paring offers a similar property like homomorphic encryption that computation over different mathematical structures can be mapped to each other. This will make the random number aggregatable and then the generation procedure asynchronous. For more details about pairings and elliptic curves, please refer to the introduction from Vitalik. For the BLS specification, please look at the document. Last but not least, the threshold version of BLS signature is robust as a decentralized system. Each time the system is asked for a random number, at most half of the group nodes need to respond. With a deliberately chosen number of group members, the availability and security of the system can both fulfill the requirement.
Comparison across verifiable random number generation:
| Verfication | Communication | Availability | Complexity | |
|---|---|---|---|---|
| Public Keyed HMAC | ECDSA | None | May abort | None |
| Threshold ECDSA | ECDSA | Several rounds | Low | Low |
| Threshold BLS | BLS | One round | High | High |
The construction of threshold BLS is pretty like executing BLS in a multi-party computation (MPC) way. Given a set of computation nodes involved in ARPA verifiable RNG, the secret key shares are distributed by Feldman’s verifiable secret sharing scheme in the key generation phase. Then each party computes and broadcasts their public key shares. The group public key can be recovered from those shares by Lagrange’s interpolation. This key represents the identity of this node set and verifies the random number generated. During the lifetime of the RNG, group secret key will never be recovered, both in key generation and random number generation.
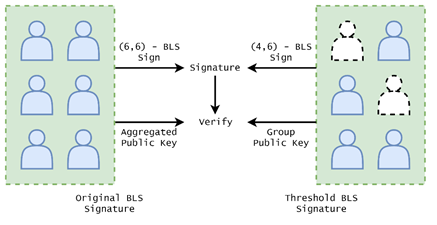
Thanks to the bilinearity of pairings, the random number generation phase is the same as the original BLS signature. Upon receiving the seed, each node computes its random number share locally and broadcasts. After the legitimacy of these shares is validated, they are aggregated by interpolating. The final result is the threshold BLS signature of the seed and then can be verified by the group public key. It should be noted that the result remains the same no matter which subset of nodes contributes the random number shares.
ARPA Decentralized RNG Architecture
Equipped with the threshold BLS signature, we can draft the architecture of ARPA verifiable RNG. Anyone running the ARPA computation node is welcomed to the RNG system. Nodes in the system are grouped based on the random number generated previously by the system. Once the groups are set, they run the distributed key generation and upload the group public key to the blockchain. After the initialization, any new random number request will be allocated to one of the groups. When the random number is generated and approved by the group, it will be sent to the smart contract that verifies it against the group public key. Taking advantage of the ETH 2.0 infrastructure, the verification should be efficient and economical.
System Robustness
The parameter of the groups is designed to fulfill the requirements of availability and security. If the secret sharing scheme employed is honest majority, then the number of total group members n=2t+1, where t is the threshold. If we set the probability of computation node failure as p, the likelihood of RNG failure can be written as:
Then we can calculate the tolerable node failure at different group size given an around 0.01% system failure ratio. It can be seen that the ratio will be reduced by increasing the group size.
Tolerable node failure vs. system failure:
| Group size | Tolerable node failure | System failure |
|---|---|---|
| 51 | 24.2% | 0.0105% |
| 101 | 31.3% | 0.0104% |
| 202 | 36.7% | 0.0106% |
| 501 | 41.6% | 0.0108% |
Besides mathematical analysis, an affiliated ecosystem can help to encourage participation and punish malicious acts.